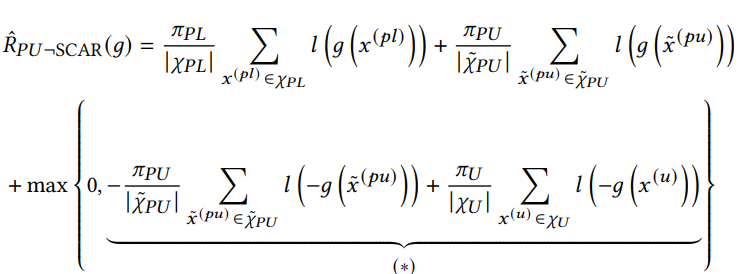https://dl.acm.org/doi/10.1145/3340531.3411971
Introduction
生成モデルを用いて、本来Nっぽいデータを生成して、それで学習するというのがある。他にもいろいろな先行研究があるが、みんなPはU分布から一様に選ばれるSelected Completely At Random仮説に立っている。
これについて、SAR仮定でも成り立つような手法を開発した。まずはSAR状況下のRisk functionを定義し、VAEを使って新しいRisk Functionでサンプルを生成し、それをうまく学習に使用するようにした。
Preliminary
- データは
- ラベルはGround-TruthがPならば、Nならばである。
- ラベルがついてるデータは、それ以外はである。
- Class Priorは
- 予測器はlogitを出力する。
- SCARでは、以下のような式を最小化する(Deep Neural Networkの都合上Objectiveが変わることがある)
- SARでは、以上の式をそのまま使うことができない。以下のような研究で、Propensity Scoreを用いて修正している。
提案手法
目標はバイアスを是正したうえでPU Learningをしたい。そのためには、Pっぽいが与えられたPの中にはないデータを生成すると考えた。
SARでも動作するアルゴリズムにするためには、ラベル付けかどうかと、Uに現れるかどうかは別々の潜在変数によって決まるという風に考える。
このため、潜在変数がどのようなふるまいをするかを定めないといけない。これはVAEで学習し生成していく。
SARにおけるRisk Function
以下のようになる。はラベル付けされたPの分布で、はラベル付けされていないPの分布。

nnPUで、max(0, ・)でclipするならば、これは以下のように、2項目の一部と三項目をclipする。
Variational PU Learning
VAE-PUは以下のようなGraphical ModelのVAEを使う。

ここで、は記述してる部分のであり、定数として枠外にあるのを定めるかたち。白枠の丸は潜在変数で、黒丸が実際に与えられるデータ。実線は生成する際の依存関係であり、点線は変分近似の関係である。はGround-Truthの潜在変数、はラベルがつくかどうかの潜在変数。はPositiveからデータを抽出してるかNegativeからデータを抽出してるかを定めるもの。
変分近似やVAEとは
事後分布の推定が難しいとき、これを別の分布で近似する。これは普通である。
与えられたデータから得られる変換した潜在変数の集合から平均や分散を得られるが、これらのパラメタをもとにどの分布がよいかを選択することがKL-Divergenceなどを最小化できるかを考えるのが、変分近似である。
VAEでは、まず入力を潜在変数にmappingする。この時、入力データ群から潜在変数の属するデータの平均や分散がわかる。その平均や分散をガウス分布(ガウス分布に従うと人間がおいてるので、通常の変分近似のように何かあるわけではない)に代入する。
この上の図では、何をもってして潜在変数の推定に使っているかを示している。
ネットワークの構造は以下の通り。白い部分が

- 左側が与えられたPデータから、ラベルがつくかどうかの変数(今までの説明では)と、そのインスタンスのがわかる。それを先ほどのGraphical Modelに従い隠れ変数を生成しそれをVAEを訓練する。(Decoderで得るができるだけ与えたと同じになるようにしたいっていうAutoEncoderの訓練)。
- 真ん中はVAEでPを生成している。(のちのち、それが
- 右側は与えられたUについて、左側と同じようになる。
- 真ん中で得たものは生成したおの、右側で得たものは与えられたUとして、Discriminatorを訓練する。
- これはGANと似ているが、GANはランダムなノイズからDecoderで復元するのに対して、VAEはガウス分布からサンプリングしてDecoderで復元している。
学習の損失関数は以下のようになる。
- GANらしく、はDiscriminator以外のネットワーク全体のパラメタで、はDiscriminatorのパラメタ。
- 交互に最小化や最大化を行う。
Generative Process and Variational Inference
具体的には以下のように設定している。
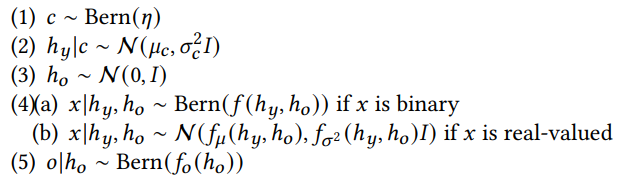
Graphical Modelから、潜在変数の分布は、以下のように得られる。
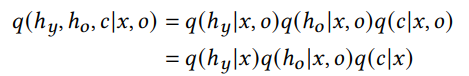

目的関数は、変分推論なのでELBOの最小化をする。ELBOは以下の式であり、Encoderは、Decoderはにあたる。
これを現在の状況にあてはめると、以下のようになる。
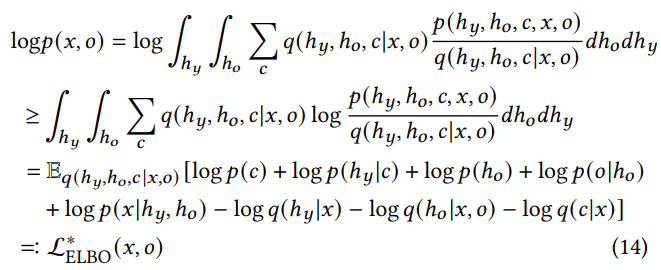
- 潜在変数の積分はの2つとの総和の1つ。
- のfirst termにあたるのは、上記のGraphical Modelから導かれた以下の同時分布。

- のsecond termは、変分推論した分布にまつわる、潜在変数3つの項。
このELBOについて、最大化していく。
実際、最大化しているとき、以下のようになる。
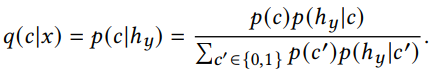
Adversarial Generation Loss
敵対的なDiscriminatorもあるので、以下のようにDiscriminatorによる損失も計算できる。この損失は単純にbinary cross entropyである。
ここがGANとの違いとして、VAEとDiscriminatorを同時に訓練している。GANは交互に訓練する。
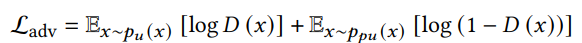
生成したPのLoss
最後に、生成したPについて、Pと判断するべきという損失である。
生成部分の全体の損失
損失は全体では、ELBO、Disriminatorのもの、生成したPのLossの3つである。
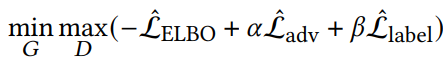
ELBO以外は明確に経験的に得ることはできる。ELBOを経験的に解くには、ランダムに数個サンプリングしてから、EncoderやDecoderの出力をもとに、経験的に条件付確率の定義から推定するしかない。
全体の流れ
アルゴリズムとしては以下の流れである。
- VAEベースの生成器を訓練する。
- ミニバッチで、が与えられる。
- 生成器で、本来存在するべきだったといわれているPデータ(バイアスがあって与えられたPの中にはなかった)を一定数生成する。
- 生成器のほうのlossを計算しアップデート
- 本命のPU Learningをおkなう。
- ミニバッチでを得る。生成器からを得る。
- 前述した、次のBiasを考慮したPUの式で学習させる。